[수학_수2] 최대 최소 극대 극소 3차 4차 함수

 

 

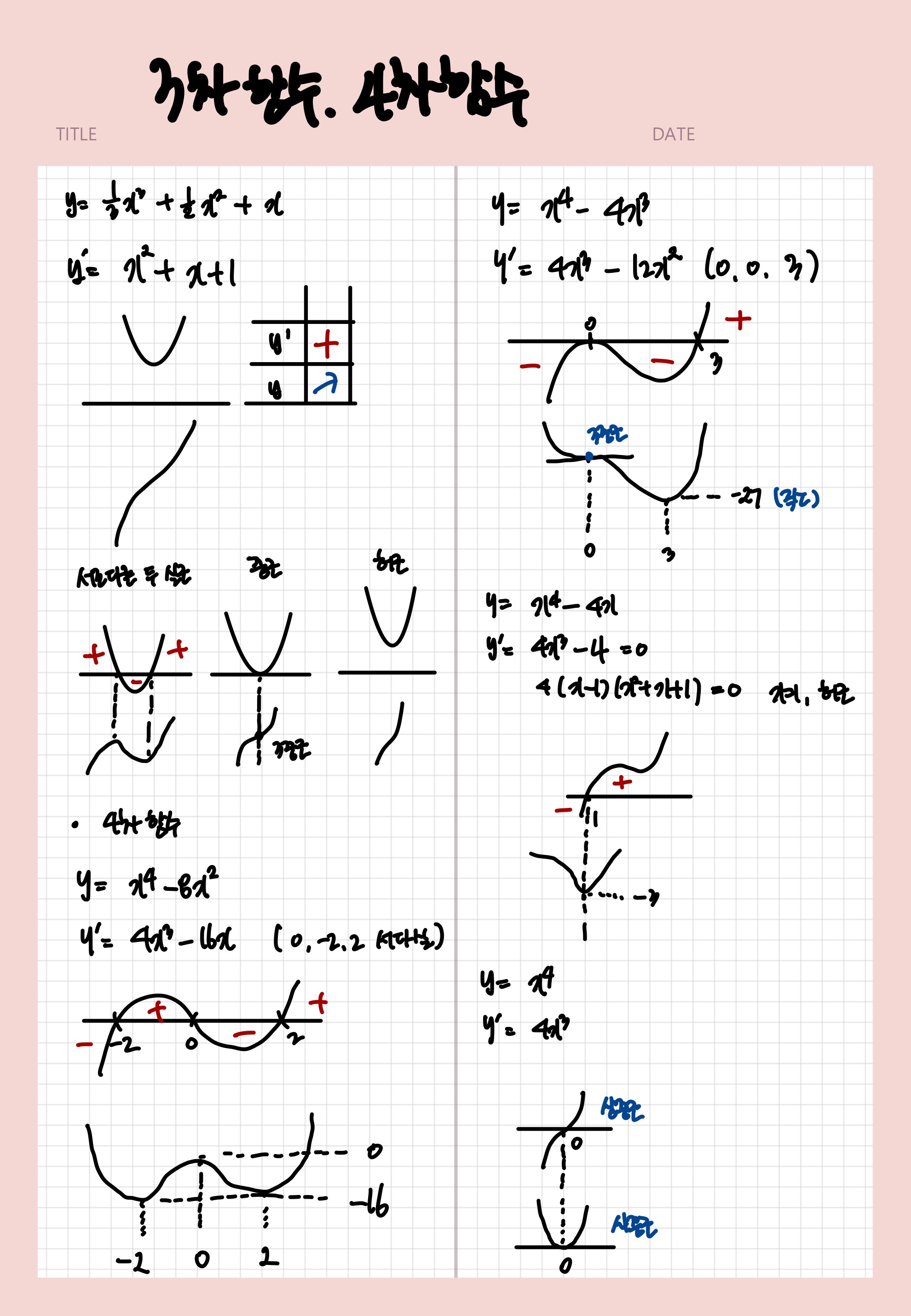
함수의 극대극소와 증가/감소 구간

1. 함수의 증가/감소

• 구간에서 증가: x₁ < x₂ → f(x₁) < f(x₂)
• 구간에서 감소: x₁ < x₂ → f(x₁) > f(x₂)

2. 극대와 극소

• 극대: 함수값이 주변보다 클 때
• 극소: 함수값이 주변보다 작을 때
• 즉, f(a-h) < f(a) > f(a+h) 이면 극대
• f(a-h) > f(a) < f(a+h) 이면 극소

3. 도함수와의 관계

• 증가 함수일 조건: f'(x) > 0
• 감소 함수일 조건: f'(x) < 0
• 극대 또는 극소일 수 있는 점: f'(x) = 0
• 단, f'(x) = 0이라고 반드시 극대/극소는 아님 (예: x³)

4. 참고 그림

위 그림은 함수의 증가/감소 구간, 극값 위치, 도함수의 부호 등을 시각적으로 잘 보여줍니다.

5. 극대, 극소, 극값

• 극값: 극대와 극소를 통틀어 부르는 말
• 극대: 함수가 그 점에서 가장 큰 값
• 극소: 함수가 그 점에서 가장 작은 값
• 극대 또는 극소가 존재하지 않더라도 도함수의 부호로 판단 가능

6. 도함수 부호판별로 극값 찾기

• 도함수 f'(x)가 0이 되는 지점을 기준으로 양수 → 음수로 바뀌면 극대
• 음수 → 양수로 바뀌면 극소
• 예: f(x) = x³ - 3x² + 2x이면 도함수는 f'(x) = 3x² - 6x + 2

7. 예제 분석

함수 f(x) = x³ - 3x² + 2x의 도함수 부호를 표로 정리하여 증가/감소와 극값 위치를 판단할 수 있다.

• 부호판별표를 활용하면 함수의 증감과 극값을 직관적으로 확인 가능
• f'(x)가 0이 되더라도 극값이 아닌 경우 존재 (예: f(x) = x³)

이런 방법은 수학 I, 미적분의 기본 개념 정리 및 그래프 해석에 매우 유용합니다.

---

💡 Tip: 극값 찾기 문제는 도함수의 부호 변화를 표로 정리하면 정확도와 속도를 모두 높일 수 있어요!