미분기하학 벼락치기 1탄_유클리드 공간, 매개곡선, 호의 길이

1.1 유클리드 공간

3차원 유클리드 공간 R^3는 세 실수의 쌍으로 이루어진 집합

(x,y,z) 이고, x,y,z는 R^3에 속함

두 점 a,b의 거리 d(a,b)는 ||a-b||

벡터합과 스칼라 곱에 대한 성질

• a+b=b+a 교환
• (a+b)+c = a+(b+c) 결합
• a+0 = a 영벡터 합해도 그대로
• a+(−a) = 0 역벡터 합하면 영벡터

• c(da) = (cd)a 결합
• (c+d)a = ca+da 분배
• c(a+b) = ca+cb 분배
• 1a = a 항등원

p.q=<p,q>=p1q1+p2q2+p3q3 내적

• ⟨a,b⟩ = ⟨b,a⟩ 교환
• ⟨ca,b⟩ = c⟨a,b⟩ 스칼라 앞으로
• ⟨a,b+c⟩ = ⟨a,b⟩ + ⟨a,c⟩ 분배
• ⟨a,a⟩ >= 0, ⟨a,a⟩ = 0 <=> a = 0
• a와b가 직교 <=> 내적<a,b>=0

놈

• ||u||>=0 영벡터일때 0
• 스칼라는 앞으로 튀어나감
• ||u+v||<=||u||+||v||

코시 슈바르츠 부등식 C.S부등식

외적

• (cu)×(dv) = (cd)(u×v) 스칼라 앞으로
• u×(v+w) = u×v+u×v 분배
• (v+w)×u = v×u+w×u 분배
• v×u = −(u×v) 교환법칙에 - 붙이기
• 0×u = 0

1.2 매개곡선

미분가능한 매개곡선 a(t)=(x(t),y(t),z(t))

무한번 미분가능 부드러운 함수

정칙곡선

• 미분가능곡선
• 미분한 것이 0이 아님

매개변수로 표현된 곡선 (접선벡터 구하기)

1. r(t)=(rcost, rsint)로 표현하기
2. 둘 다 0이 나오는 t 값 구하기
3. r'(t) 구한다. 각각 t에 대해 미분하면 됨
4. 0이나오는 t 값 r'(t)에 대입하면 그게 접선벡터

1.3 곡선의 길이(호장)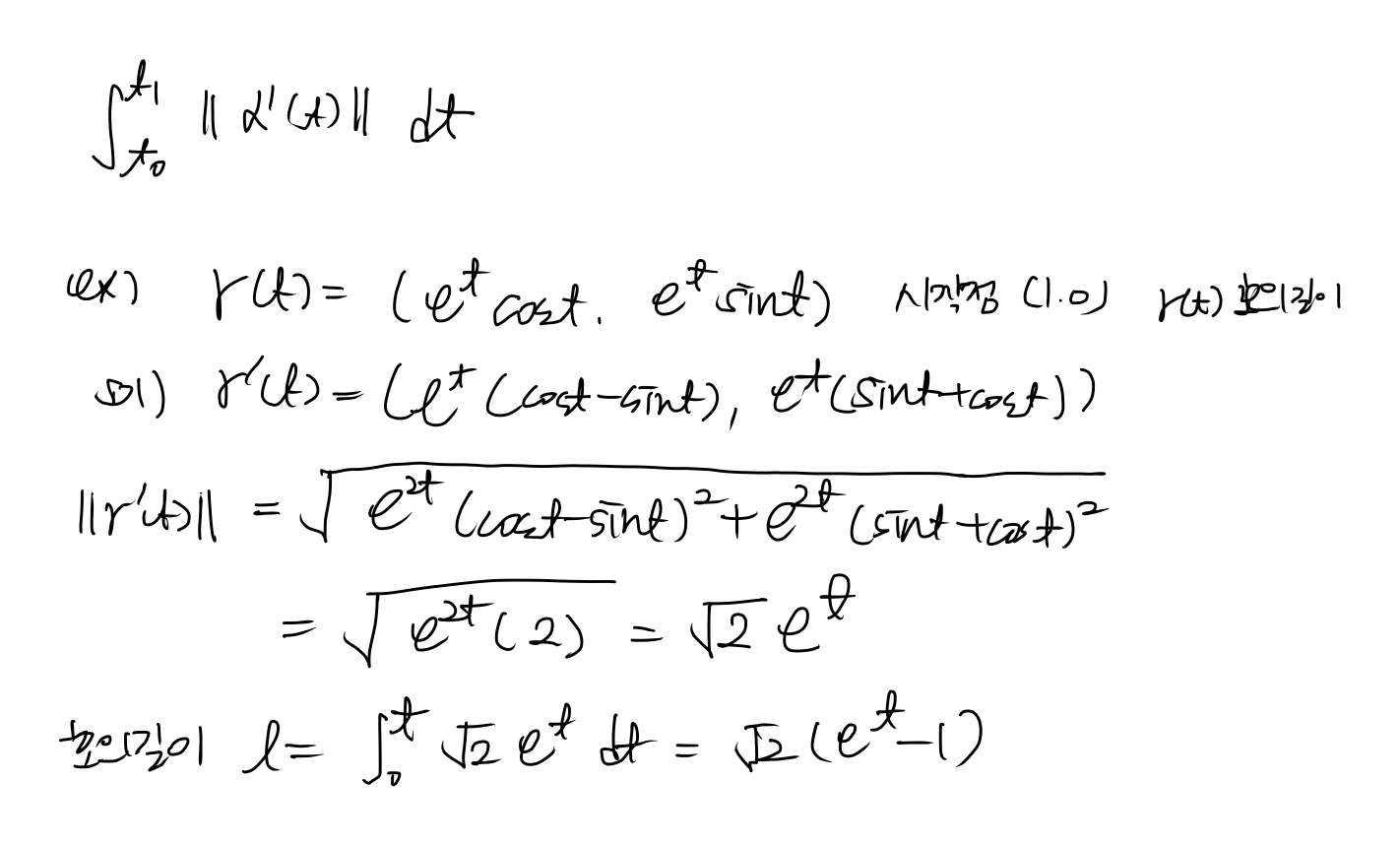

재매개화(합성함수 느낌적인느낌느낌)

1. 호장함수 구함
2. 속력구함
3. t의 식으로 정리하고 대입함

선적분