[수2_미분] 2. 미분 가능성과 연속성
이번 단원에서는 미분이 가능한지를 따짐
일단 개 간단하게
미분 가능 → 연속임
연속임 ↛ 미분 가능함 이거임
이거 알라면 지난 단원인
미분 계수와 도함수 이걸 알아야 함
https://sudamilda.tistory.com/186
[수2_미분] 1. 미분계수와 도함수
직선의 기울기부터 스타트참고로 미분은 간단히 기울기다 아아 한 점과 다른 한 점을 이은그 선의 기울기를 나타내는 것은 세가지가 있다. 1. y 차이 / x 차이 (여기서 차이가 델타임)2. 그걸
sudamilda.tistory.com
어쨌든 지난 단원 안다고 치고 설명함
미분 가능성 따지려면 개 간단하게
우미분계수 = 좌미분계수 이렇게 따지면 됨
그게 곧 미분 계수가 존재한다는 의미 아니겠음
그래서 한 번은 x가 a로 가까이 갈 때의 식
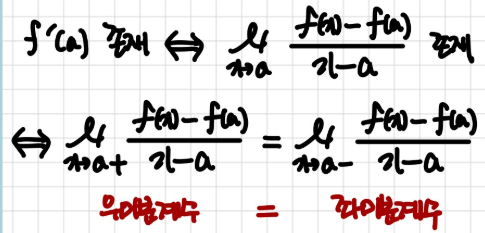
또 한 번은 h가 0으로 가까이 갈 때의 식
h를 델타x로 써도 되는거 알지?
모르면 1단원 다시보셈
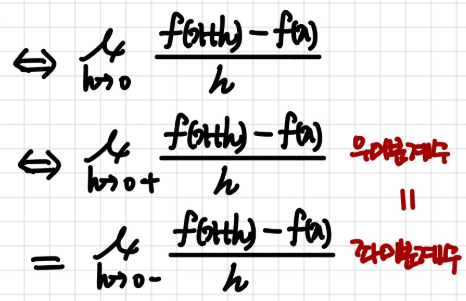
그래서 사실상 문제는 미분계수 우극한
미분계수 좌극한 구해서 같은지 확인하면 됨
그럼 이 단원은 사실상 끝임

그래서 미분 불가능한 점은 크게 두 가지 있음
첫 번째, 불연속 점
이건 당연한게 미분 가능함 → 연속임 이니까
대우 명제 사용하면 불연속임 → 미분 불가능함 임
두 번째, 뾰족한 점
이건 식으로 봐도 되지만,
그림으로 봐도 괜찮음
왼쪽 그래프는 기울기가 마이너스지만,
오른쪽 그래프는 기울기가 쁠라스임
뭐 구하고 말거 할거 없이 걍 다름
그래서 미분 불가 귀찮아서 미불이라고도 함

예시 문제를 풀어보자
y=|x-3| 이 그래프인데
이거 그리는 방법은 다들 아시는가?
x≥3 일 때, y=x-3
x<3 일 때, y=-(x-3)=-x+3
그래서 그림 그리면 저렇게 나옴
뾰족하게 어디서? x=3기점으로 기울기가 달라짐
그래서 그래프만 그려보면 바로 아
미분 계수가 다르겠구나~
알 수 있음 그걸 식으로도 풀어보면 다음과 같음
식을 다 풀어보면
좌미분계수와 우미분계수가 다름
따라서 미분 불가
하지만 어떤 절대값 있는 함수는
미분이 가능하기도 하니
절대값만 보고 바로 미불이라고 판단하지는 말자!

