[수2] 미분-평균값정리

롤의 정리

함수 f(x)가 닫힌 구간 [a,b]에서 연속이고,

열린구간 (a,b)에서 미분 가능이며

f(a) = f(b) 이면 f'(c)인 c가

(a,b) 사이에 적어도 하나 존재

 

쉽게 생각하면 평균값 정리에서

양 끝값이 같은 특이한 case

평균 변화율이 0인 특이 case

 

 

양 끝의 함수값이 같으므로

양 끝을 이은 직선의 기울기가 0이된다.

 

이 곡선의 접선 중

접선의 기울기가 0인 점이

(a,b)사이에 적어도 1개 존재한다. 

 

이것이 롤의 정리이다. 

 

 

문제로 보면 더 간단한데

 

 

그냥 미분 때린후에

기울기 = 0 인 값을 찾으면 끝이다. 

 

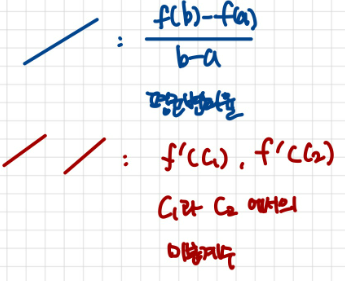
평균값의 정리

함수 f(x)가 닫힌 구간 [a,b] 연속이고

열린구간 (a,b)에서 미분가능하면

평균변화율과 미분계수가 같게되는

c가 열린구간 (a,b)에 적어도 하나 존재한다. 

 

 

그림을 살펴보면,

 

 

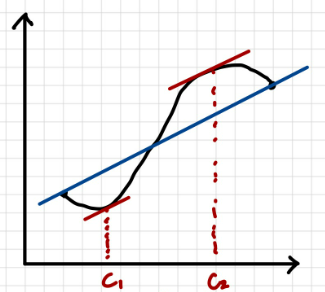
양 끝값을 이은 직선의 기울기는

평균변화율이다. 

 

그것이 파란 직선이다. 

 

 

헌데 파란 직선과 기울기가 같은

빨간직선,

 

즉, 접선의 기울기가 평균 변화율과 같아지는

점이 존재하게 된다. 

그것이 평균값 정리이다.

 

문제를 풀때는 평균변화율=미분계수 하고 풀면 끝